Abstract
- Based on the IEEE 754 Standard
- sign 0 for positive, 1 for negative
- exponent by default -127 with all bits set to 0. If we want positive, we need to set the 8th bit to
1which is128 - mantissa takes the binary behind the decimal place after normalisation (the yellow circle part)
- Reliable precision is 7 decimal digits

Approximation of Real Number
- mantissa gives the precision
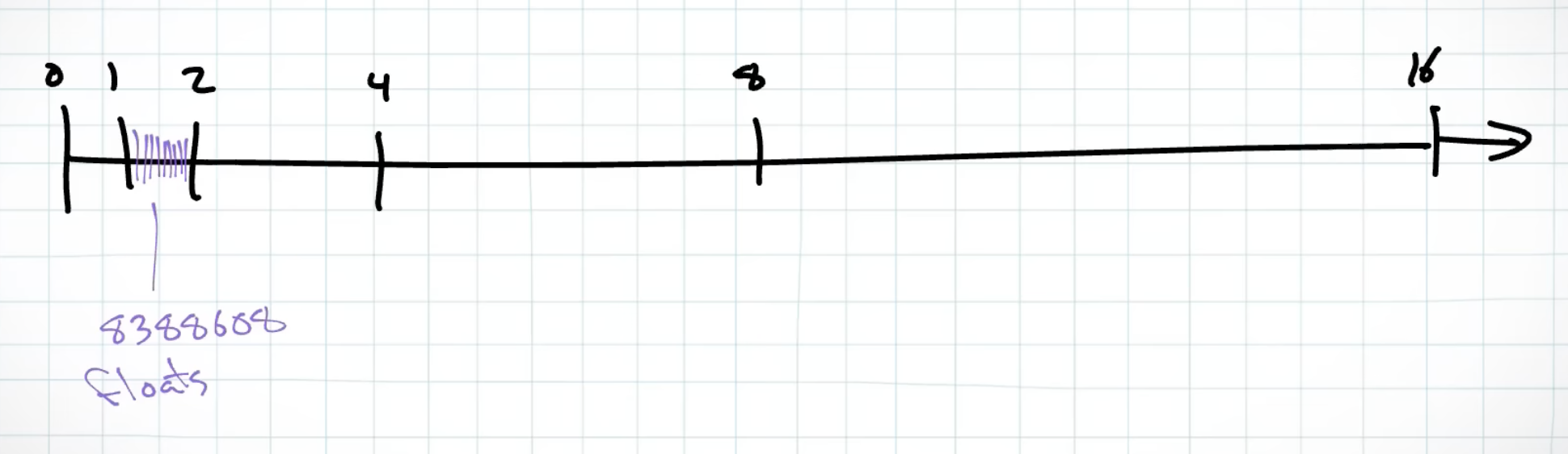
- From 1 to 2 (2^0-2^1), there are 23 bits of mantissa used for precision after decision point
- For 2 to 4 (2^1-2^2), there are 22 bits of mantissa used for precision after decision point, one of the bit is used to present the whole number before decimal point
- With every range of 2, the precision after the decimal point is reduced by 2
- Thus, the precision of the number after decimal point is getting worse as the number getting bigger
Normalised Number
- The range of real numbers between 0 and smallest Normalised Number isn’t covered, covered by Subnormal Number (Denormalized Number)

- The 1 is implicit when exponent isn’t 0. When exponent is 0, we get Subnormal Number (Denormalized Number)

Smallest positive Normalised Number
- One bit for exponent to differentiate from Subnormal Number (Denormalized Number)

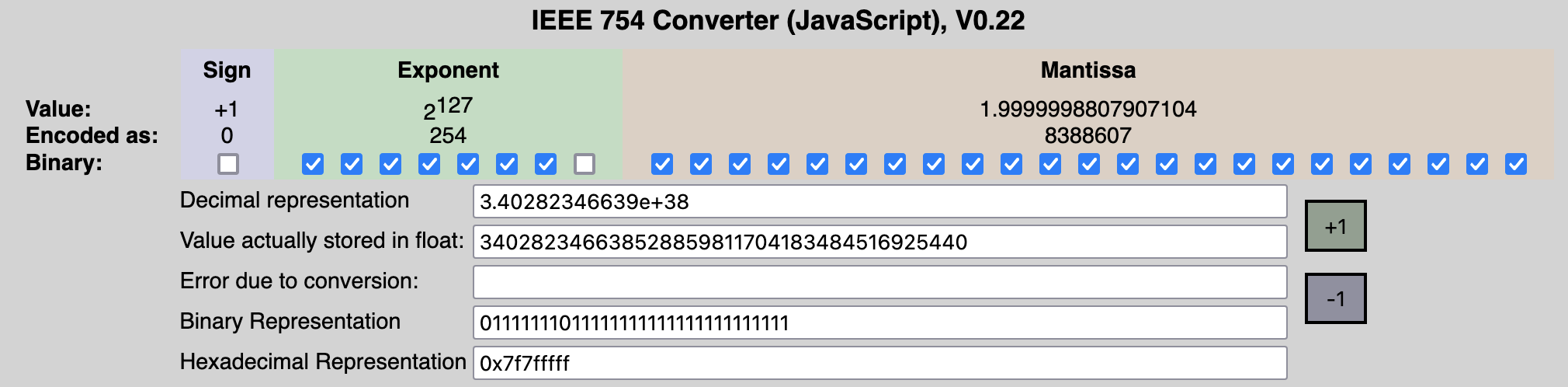
Biggest positive Normalised Number
- All 1s for exponent means Infinity
Subnormal Number (Denormalized Number)
- Fill up the gap between 0 and the smallest Normalised Number
- Without, we will get a 0 if the difference between 2 numbers is smaller than the smallest Normalised Number

In non-debug mode, Subnormal Number maybe turned off for performance reasons, and this may lead to unexpected errors
Smallest positive Subnormal Number (Denormalized Number)
- The exponent bias is fixed at -126 when denormalised, and 0 is implicit instead of 1

Biggest Subnormal Number (Denormalized Number)
- 0 when Mantissa bits are all 0

3 Special Cases
0
- Both Exponent & Mantissa is 0

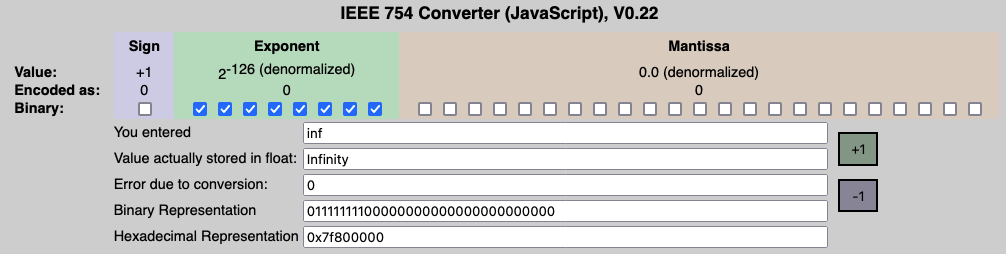
Infinity
- Exponent is 255, but Mantissa is 0
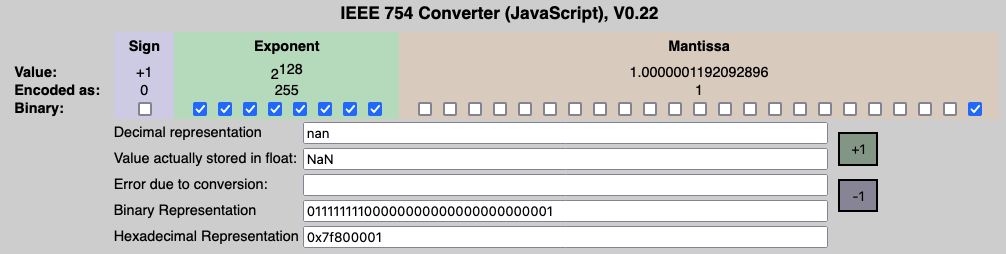
NaN
- Exponent is 255 & Mantissa isn’t 0
Tips
- When it comes to store a large whole number, use
longto represent, because floating options likedoublemay have precision loss issues - Usually Binary to Hex for better readability
- Online Converter to visualise better
Side Notes
Floating-point rounding error
- Binary representation that requires infinite precision
- Decimal number like 0.1 in binary representation is like 1/3 in decimal presentation. With limited precision (32bits), we will lose some precision. That is why 0.1+0.2 in binary isn’t strictly 0.3
References
- Wait, so comparisons in floating point only just KINDA work? What DOES work?
- Why Is This Happening?! Floating-point rounding error
