Algorithm Complexity Analysis

Abstract

---

• Analysis space & time used, related with the input size and observing the trend when input size gets bigger
• The analysis isn’t limited to particular machine. It applies to all the machines

Asymptotic Analysis

---

Asymptotic

We only cares about what is the complexity when the input size is approaching Infinity (∞), that is where the name asymptotic comes from.

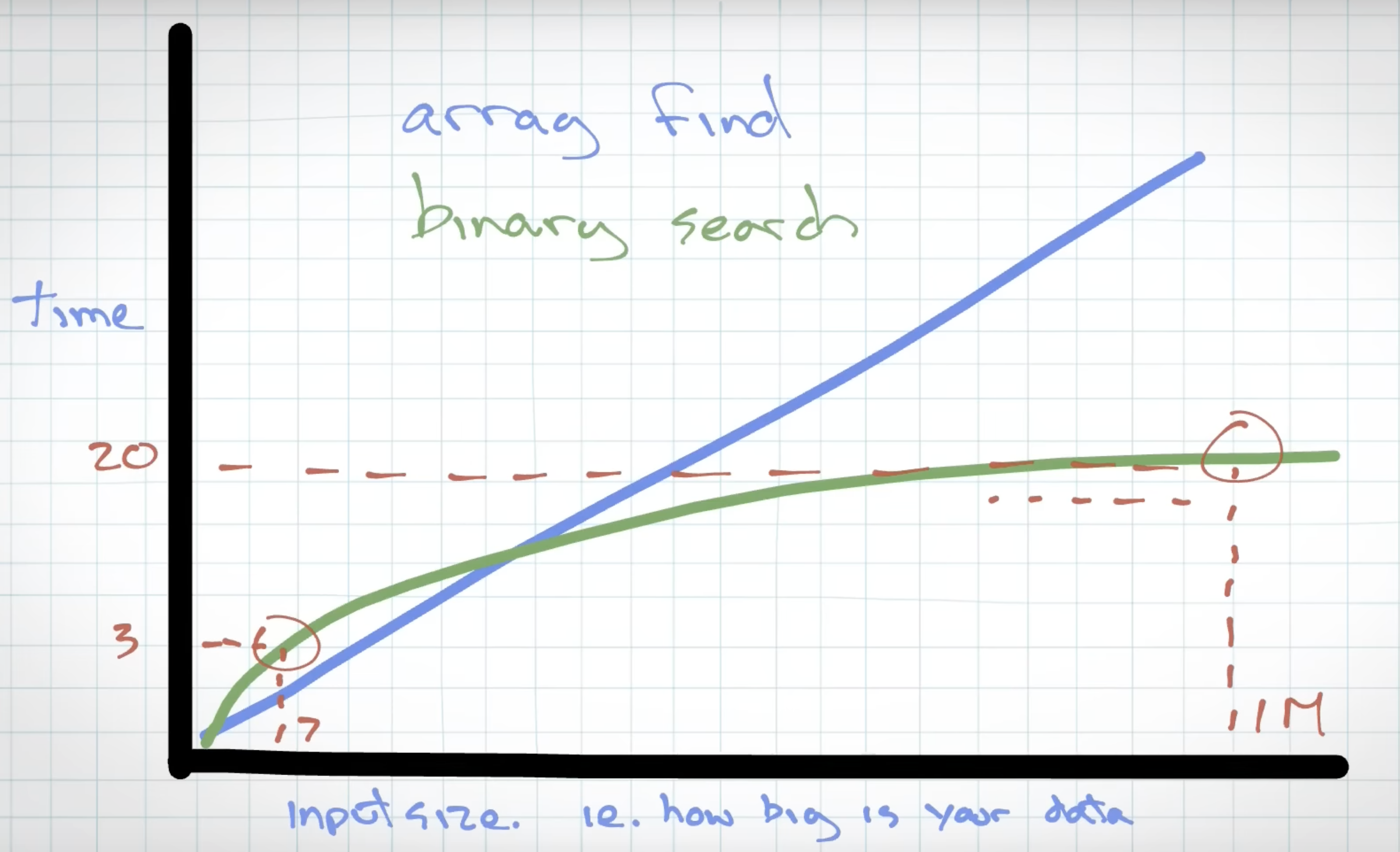
So when the actual input size in real world is small, the algorithms with worst time complexity may run fast!

• Asymptotic Analysis doesn’t return some good approximations of the time the program takes to run. We mean the time taken by the program bounded by some constant $\times$ a function when the input size is bigger than a certain constant
• $O()$ represents the upper bound
• $\Theta ()$ represents the space in between upper bound and lower bound
• $\Omega ()$ represents the lower bound

Determine tightest upper bound (in terms of n)

1. Take the most dominant term and drop the coefficients
2. If 2 terms with $n$ multiplying each other, they are one piece

Use codes to find algorithm complexity analysis

We can write out the given program, then place a counter at the core part of the program. Then we can obtain the relationship by observing the value we substituted to the input and the value of the counter

Tricky ones to evaluate tightest upper bound!

$4n^{2}log(n)$

• $O(n^2)$ is wrong because $log(n)$ isn’t a constant, $O(n^2)$ is going to be a lower bound
• $O(n^{2}logn)$ is the valid tightest upper bound. The next tightest upper bound is $O(n^3)$

$f(n{)}^{g(n)}$, where $f(n)=O(n)$, $g(n)=O(logn)$

• Cant determine! Because the constant matters in the exponent here
• For example, when $g(n)=logn$, then $f(n{)}^{g(n)}=n^{logn}$, when $g(n)=2logn$, then $f(n{)}^{g(n)}=n^{2logn}=(n^{logn}{)}^2$
• $(n^{logn}{)}^2$ is significantly slower than $n^{logn}$!

$2^{2n}$

• $O(2^n)$ is wrong, because $2^{2n}=(2^n{)}^2$, the $2$ raises the complexity one magnitude. It isn’t same as $O(2\times 2^n)$ in which we can ignore the constant $2$

$log(n!)$

• The answer is $O(nlogn)$, don’t have the math knowledge yet to further explain :(

Evaluate time complexity of if/else

Lets $f$ be the cost of first, and $s$ be the cost of second

$$Cost=max(f,s)\le f+s$$

Worst Space Complexity

• The Main Memory used relative to the input size

2 ways to count

Maximum space every allocated at one time

• The amount of space the algorithm needs to run

Total space ever allocated

• The total amount of space algorithm uses to run the algorithm. We need to consider this because memory allocation is an expensive operation

Worst Time Complexity

• The time it takes relative to the input size

References

---

• SimonDev - YT
• Hello-algo - YT
• Back to Back SWE - YT