Mathematical Function

Abstract

---

• A special type of Relation where each input value maps to exactly one output value. In relation, we can have an element that is a parent of one or more other elements

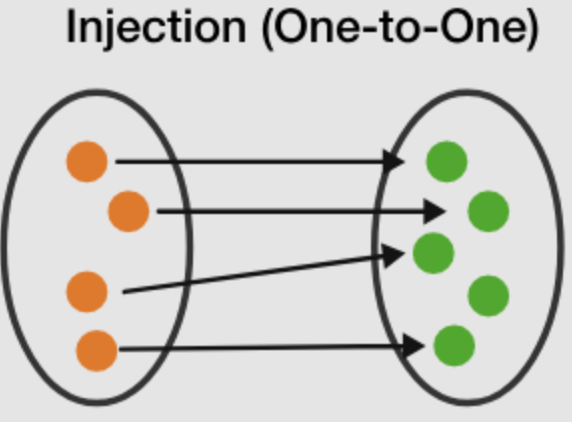
Injective

Each element in the Domain maps to a distinct element in the Co-domain.

Surjective

Every element in the codomain is covered by the function. However, the function shown in the diagram below isn’t injective, since 2 inputs point to the same output.

Bijective

When a function is both injective & surjective. When a function has a Inverse Function, we can say it is bijective. Since inverse function uses the codomain of the original function as domain - surjective & inverse function follows the rule of function, each input maps to exactly one output - this shows no input value from the original function maps to more than one output, thus injective.

Inverse Function

---

• A Mathematical Function that essentially undoes the action of the original function

Example

Given $f(x)=2x$, then $f^{-1}(x)=\frac{x}{2}$.

If $x=3$, then $f(3)=6$, $f^{-1}(x)=\frac{6}{2}=3$.

Visual relationship with function

Inverse function is basically a reflection of the original function about the line $y=x$

Real-value function

---

• A Mathematical Function that assigns Real Number as outputs for real numbers as inputs. In other words, it’s a function where both the Domain and the Co-domain are Subset of the real numbers

Polynomial Function

---

$$f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_2{x}^2+a_{1}x+a_0$$

• $a$ is constant, and the polynomial function above is called polynomial of degree $n$

Attention

A polynomial of degree $n$ can be factored as a product of linear and quadratic Factor.

For example, $x^4-1=(x^2+1)(x+1)(x-1)$, where $(x+1)$ and $(x-1)$ are linear factors and $(x^2+1)$ is quadratic factor.

Rational Function

$$\frac{p(x)}{q(x)}$$

• Both $p(x)$ and $q(x)$ are Polynomial Function
• The Domain of $\frac{p(x)}{q(x)}$ consists of all Real Number except the root of $q(x)$ - the value of $x$ that will make $q(x)=0$