Binary Search Tree (二叉搜索树)

Abstract

---

• Also known as BST
• Nodes have a value attached to it. If the left sub-tree isn’t empty, all nodes on that sub-tree is smaller than the value of Root Node. If the right sub-tree isn’t empty, all nodes on that sub-tree is bigger than the root node value. Its left sub-tree and right sub-tree are also binary search tree

Access previous node from current node

Use a variable prevNode to keep track of the previous node. Handy in solving some problems.

Practice questions

• 98. Validate Binary Search Tree
• 108. Convert Sorted Array to Binary Search Tree

BST Node Traversal

---

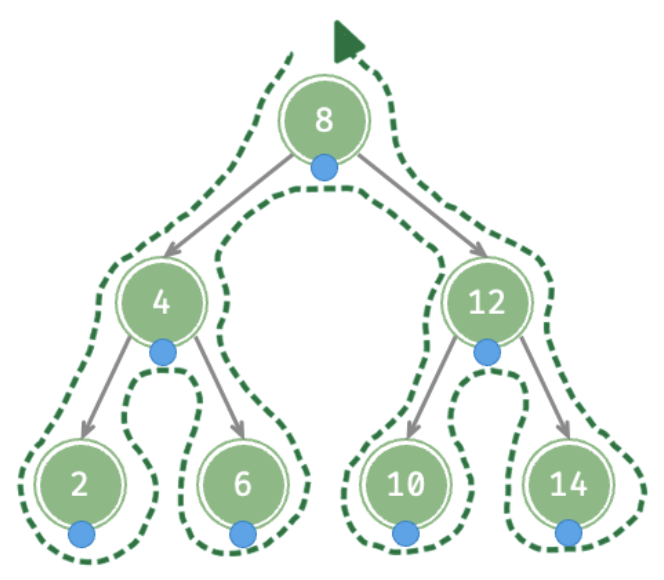
• We can use In-Order Traversal to print the nodes inside a BST from smallest to the biggest or from biggest to smallest with $O(n)$

From smallest to the biggest

Go to the left subtree then right subtree. Useful in finding the minimum absolute difference among the nodes

From biggest to the smallest

Go to the right subtree then left subtree. Useful in converting the BST to Greater Tree.

BST Node Search

---

Attention

We can only achieve $log(n)$ if the BST is Height-Balanced. A not height-balanced BST can be degraded into a Degenerate Binary Tree.

• If the current node isn’t the node we are finding, select the node.left when target value is smaller than the current node, otherwise select node.right
• This allows us to choose only one side of the Binary Search Tree (二叉搜索树) at each Level, achieving $log(n)$ speed

Practice questions

• 700. Search in a Binary Search Tree

BST Node Insertion

---

Attention

We can only achieve $log(n)$ if the BST is Height-Balanced. A not height-balanced BST can be degraded into a Degenerate Binary Tree.

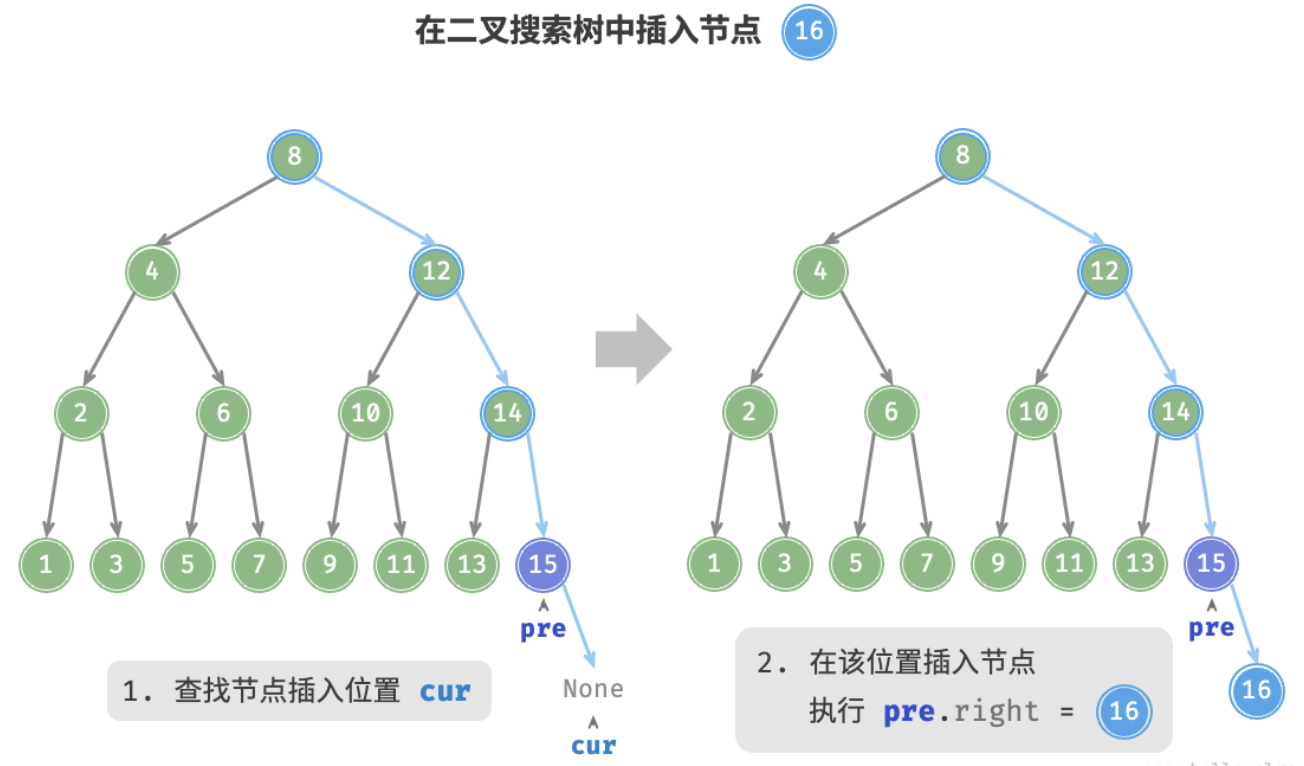
• The idea is to insert the new node as a Leaf Node to minimise modification to the Binary Search Tree (二叉搜索树)
• The suitable null slot can be found in $log(n)$ speed by going down the BST using the BST Node Search

Practice questions

• 701. Insert into a Binary Search Tree

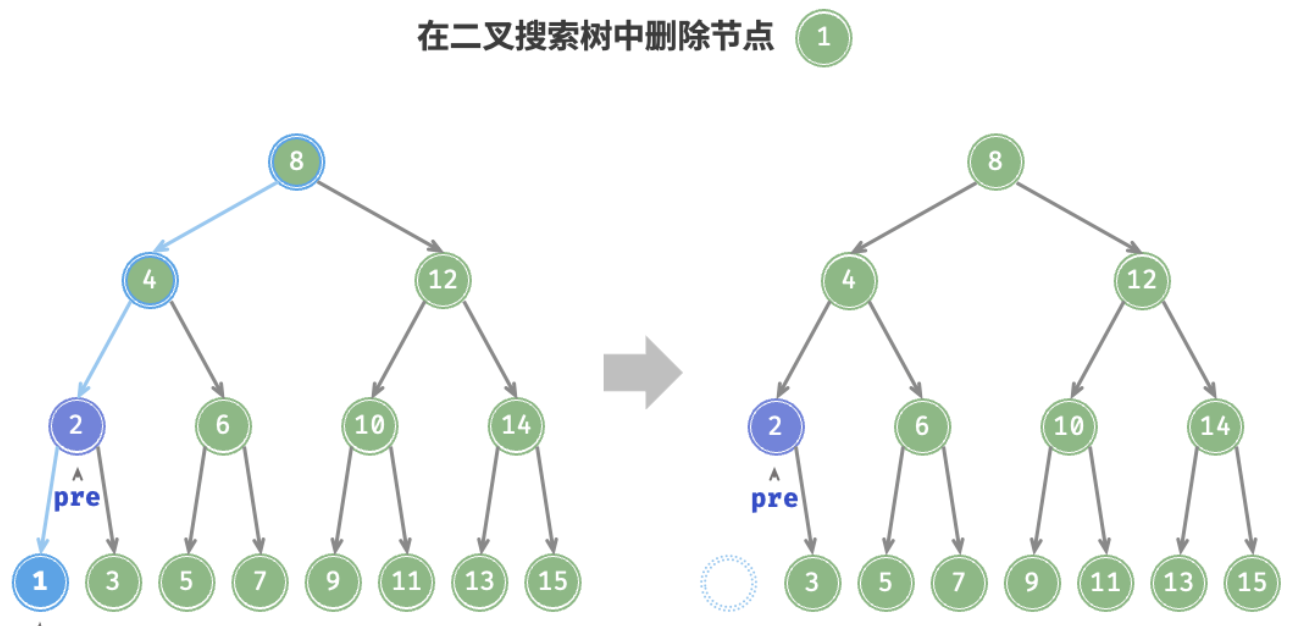
BST Node Deletion

---

• When the Degree of the deleted node is $0$, we can just remove it without any other modifications

/* 
pre is the parent node of the deleted node
root is the root node of the binary search tree
cur is the deleted node
*/
 
TreeNode child = cur.left != null ? cur.left : cur.right;
// delete node
if (cur != root) {
  if (pre.left == cur)
    pre.left = child;
  else pre.right = child;
} else {
  // if the deleted node is the root node，we assign its child node as the new root node
  root = child;
}

• When the Degree of the deleted node is $1$, we can just need to smallest node from its right subtree without any other modifications

/* 
pre is the parent node of the deleted node
root is the root node of the binary search tree
cur is the deleted node
*/
 
TreeNode child = cur.left != null ? cur.left : cur.right;
// delete node
if (cur != root) {
  if (pre.left == cur)
    pre.left = child;
  else pre.right = child;
} else {
  // if the deleted node is the root node，we assign its child node as the new root node
  root = child;
}

• When the Degree of the deleted node is $2$, we can just need to replace it with smallest node from its right subtree or the biggest node from its left subtree. Below shows replacing the deleted node with the smallest node from its right subtree

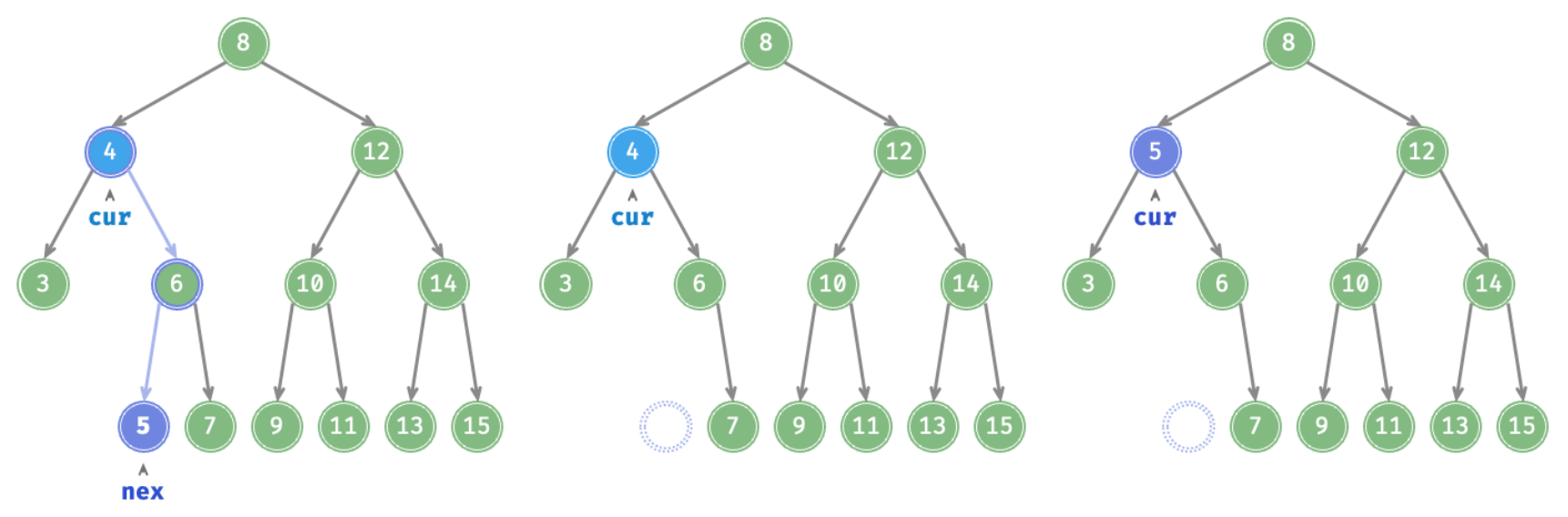
// cur is the deleted node
 
// finding the smallest node from deleted node's right subtree, and assign it to tmp
TreeNode tmp = cur.right;
while (tmp.left != null) {
  tmp = tmp.left;
}
 
// Delete tmp from the right subtree of the deleted node, the remove() implementation is same as delete node that has a degree of 0
remove(tmp.val);
// replace the deleted node with the smallest node from its right subtree
cur.val = tmp.val;

• We can encapsulate the logic of BST node deletion in the three situations described above into a single remove() function

/*
pre is the parent node of the deleted node
root is the root node of the binary search tree
cur is the deleted node
*/
 
void remove(int num) {
  // if tree is empty, no node to delete, terminate the remove() operation
  if (root == null) return;
  
  TreeNode cur = root, pre = null;
  
  // Find the deleted node - curr
  while (cur != null) {
    // Deleted node found! Proceed to deletion
    if (cur.val == num) break;
    
    pre = cur;
    // Since the value of deleted node is bigger, go to right subtree to find the deleted node
    if (cur.val < num)
      cur = cur.right;
    // Since the value of deleted node is smaller, go to left subtree to find the deleted node
    else cur = cur.left;
  }
  
  // Deleted node not found, terinate the remove() operation
  if (cur == null) return;
  
  // The degree of deleted node is 0 or 1
  if (cur.left == null || cur.right == null) {
    TreeNode child = cur.left != null ? cur.left : cur.right;
    // delete node
    if (cur != root) {
      if (pre.left == cur)
        pre.left = child;
      else
        pre.right = child;
    } else {
      // if the deleted node is the root node，we assign its child node as the
      // new root node
      root = child;
    }
  }
  // The degree of deleted node is 2
  else {
    // finding the smallest node from deleted node's right subtree, and assign
    // it to tmp
    TreeNode tmp = cur.right;
    while (tmp.left != null) {
      tmp = tmp.left;
    }
 
    // Delete tmp from the right subtree of the deleted node, the remove()
    // implementation is same as delete node that has a degree of 0
    remove(tmp.val);
    // replace the deleted node with the smallest node from its right subtree
    cur.val = tmp.val;
  }

Practice questions

• 450. Delete Node in a BST

Leetcode Question

---

Properties

• 530. Minimum Absolute Difference in BST
• 501. Find Mode in Binary Search Tree

Modification & Structure

• 669. Trim a Binary Search Tree

Common Ancestor

• 235. Lowest Common Ancestor of a Binary Search Tree

Terminologies

---

Greater Tree

• Every value of node of the original BST is changed to the original value of node plus the sum of all value of nodes greater than the value of the original node of in BST

Practice questions

• 538. Convert BST to Greater Tree

References

---

• 7.4   二叉搜索树 - Hello 算法