Abstract

- Based on the IEEE 754 Standard
- Sign: indicates a positive number, indicates a negative number
- Exponent: Comes with a bias of , represented by all exponent bits set to 0. To obtain a positive exponent, set the 8th (most significant) bit to
1, resulting in a value of128 - Mantissa: This represents the fractional part of the number after normalisation. The binary digits following the decimal point are included in the mantissa.
Why make it so complicated?
A more intuitive way to represent numbers with decimal points is to use fixed-point, where we allocate a certain number of bits for the whole number part and a certain number of bits for the fractional part. However, floating-point encoding allows us to use the same number of bits to represent both very large and very small numbers, with high precision thanks to the use of exponent.
How Mantissa Precision Varies with Exponent
The mantissa in IEEE 754 floating-point representation determines the precision of a number. Let’s analyze how precision changes across different ranges:
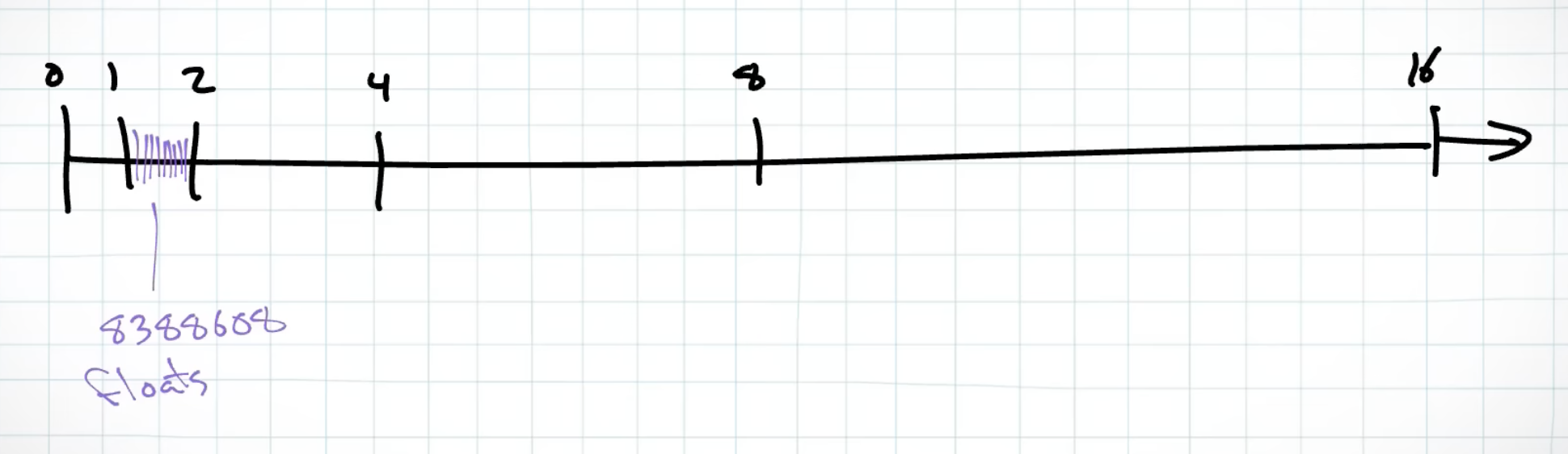
- Range 1 to 2 ( to ): All 23 bits of the mantissa contribute to the precision after the decimal point.
- Range 2 to 4 ( to ): One bit is used to represent the whole number (2) before the decimal point, leaving 22 bits for precision after the decimal.
- Generalisation: For every increase in the exponent by 1 (doubling the range), the precision after the decimal point decreases by a factor of 2. This is because one more bit is allocated to representing the whole number part.
Tip
To store large whole numbers, use the
longdata type. Floating-point options likedoublemay introduce precision loss.For improved readability, convert binary representations to hexadecimal.
Here is an Online Converter to help visualising the floating-point encoding better.
Why 0.1 + 0.2 = 0.30000000000000004?
For numbers whose binary representation requires infinite precision, like the decimal number , the binary equivalent is analogous to representing in decimal form.
With limited precision (e.g., 32 bits), we inevitably lose some accuracy. This is why 0.1 + 0.2 in binary floating-point arithmetic does not strictly equal 0.3.
Approximation destroys associativity
Given 3 floating points number , and , , which is same as .
Associativity is not guaranteed with floating-point numbers because each operation may produce an approximated value.
Converting from Decimal to Float (IEEE 754 Single Precision)
- Convert Decimal to Binary
- Convert the binary form to normalised form
- Calculate the Exponent Field by adding the bias to the exponent & convert the sum to binary (8 bits)
- Determine the Sign Bit, for positive, for negative
- Assemble the Float
- Convert to Hexadecimal by grouping the 32 bits into groups of 4, and convert each group to its hexadecimal equivalent
Normalised Number

- In the context of Floating-Point Encoding (浮点数编码), a normalised number is one where the leading digit (the digit to the left of the decimal point) is always . This is not explicitly stored but is implicit, thus one more bit for the mantissa for a higher accuracy
Important
The range of real numbers between and the Smallest Positive Normalised Number is not covered by normalised numbers, but by subnormal numbers.
The leading 1 is implicit in normalised numbers when the exponent is not zero. When the exponent is zero, we have a subnormal number, and the implicit leading 1 is no longer assumed.
Smallest Positive Normalised Number

- One bit for exponent to differentiate from Subnormal Number
Biggest Positive Normalised Number
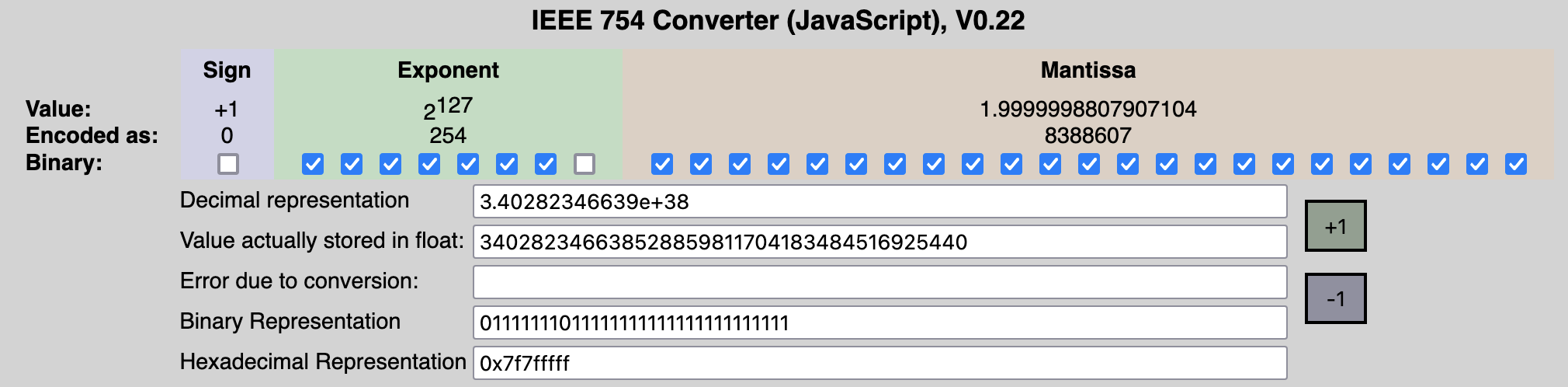
- All 1s for exponent means Infinity
Subnormal Number
- Also known as Denormalised Number
- Fill up the gap between 0 and the smallest Normalised Number
- Without, we will get a 0 if the difference between 2 numbers is smaller than the smallest normalised number

Caution
In non-debug mode, subnormal number maybe turned off for performance reasons, and this may lead to unexpected errors.
Smallest Positive Subnormal Number
- The exponent bias is fixed at -126 when denormalised, and 0 is implicit instead of 1

Biggest Positive Subnormal Number
- 0 when Mantissa bits are all 0

3 Special Cases
0
- Both Exponent & Mantissa is 0

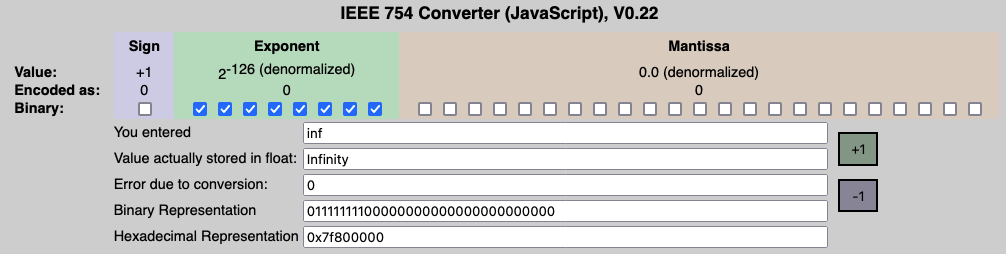
Infinity
- Exponent is 255, but Mantissa is 0
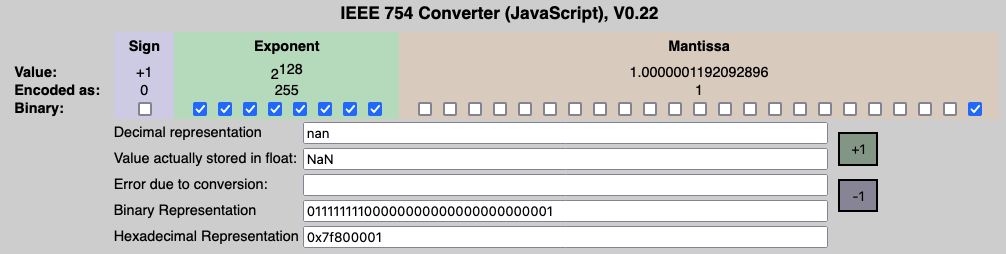
NaN
- Exponent is 255 & Mantissa isn’t 0